
Below we explain some key terms used in this tutorial.
- FEniCS: name of a software suite composed of many individual software
- components (see fenicsproject.org). Some components are DOLFIN and Viper, explicitly referred to in this tutorial. Others are FFC and FIAT, heavily used by the programs appearing in this tutorial, but never explicitly used from the programs.
- DOLFIN: a FEniCS component, more precisely a C++ library, with
- a Python interface, for performing important actions in finite element programs. DOLFIN makes use of many other FEniCS components and many external software packages.
- Viper: a FEniCS component for quick visualization of finite element
- meshes and solutions.
- UFL: a FEniCS component implementing the unified form language
- for specifying finite element forms in FEniCS programs. The definition of the forms, typically called a and L in this tutorial, must have legal UFL syntax. The same applies to the definition of functionals (see the section Computing Functionals).
- Class (Python): a programming construction for creating objects
- containing a set of variables and functions. Most types of FEniCS objects are defined through the class concept.
- Instance (Python): an object of a particular type, where the type is
- implemented as a class. For instance, mesh = UnitInterval(10) creates an instance of class UnitInterval, which is reached by the name mesh. (Class UnitInterval is actually just an interface to a corresponding C++ class in the DOLFIN C++ library.)
- Class method (Python): a function in a class, reached by dot
- notation: instance_name.method_name
- argument self (Python): required first parameter in class methods,
- representing a particular object of the class. Used in method definitions, but never in calls to a method. For example, if method(self, x) is the definition of method in a class Y, method is called as y.method(x), where y is an instance of class Y. In a call like y.method(x), method is invoked with self=y.
- Class attribute (Python): a variable in a class, reached by
- dot notation: instance_name.attribute_name
Most classes in FEniCS have an explanation of the purpose and usage that can be seen by using the general documentation command pydoc for Python objects. You can type
pydoc dolfin.X
to look up documentation of a Python class X from the DOLFIN library (X can be UnitSquare, Function, Viper, etc.). Below is an overview of the most important classes and functions in FEniCS programs, in the order they typically appear within programs.
UnitSquare(nx, ny): generate mesh over the unit square
![[0,1]\times [0,1]](_images/math/ac8e6ab5cdf1c6a6e37ea0439ed75612939e0abb.png) using nx divisions in
using nx divisions in 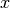 direction and
ny divisions in
direction and
ny divisions in 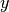 direction. Each of the nx*ny squares
are divided into two cells of triangular shape.
direction. Each of the nx*ny squares
are divided into two cells of triangular shape.
UnitInterval, UnitCube, UnitCircle, UnitSphere, Interval, Rectangle, and Box: generate mesh over domains of simple geometric shape, see the section Creating More Complex Domains.
FunctionSpace(mesh, element_type, degree): a function space defined over a mesh, with a given element type (e.g., 'Lagrange' or 'DG'), with basis functions as polynomials of a specified degree.
Expression(formula, p1=v1, p2=v2, ...): a scalar- or vector-valued function, given as a mathematical expression formula (string) written in C++ syntax. The spatial coordinates in the expression are named x[0], x[1], and x[2], while time and other physical parameters can be represented as symbols p1, p2, etc., with corresponding values v1, v2, etc., initialized through keyword arguments. These parameters become attributes, whose values can be modified when desired.
Function(V): a scalar- or vector-valued finite element field in the function space V. If V is a FunctionSpace object, Function(V) becomes a scalar field, and with V as a VectorFunctionSpace object, Function(V) becomes a vector field.
SubDomain: class for defining a subdomain, either a part of the boundary, an internal boundary, or a part of the domain. The programmer must subclass SubDomain and implement the inside(self, x, on_boundary) function (see the section Implementation (1)) for telling whether a point x is inside the subdomain or not.
Mesh: class for representing a finite element mesh, consisting of cells, vertices, and optionally faces, edges, and facets.
MeshFunction: tool for marking parts of the domain or the boundary. Used for variable coefficients (“material properties”, see the section Working with Two Subdomains) or for boundary conditions (see the section Multiple Neumann, Robin, and Dirichlet Condition).
DirichletBC(V, value, where): specification of Dirichlet (essential) boundary conditions via a function space V, a function value(x) for computing the value of the condition at a point x, and a specification where of the boundary, either as a SubDomain subclass instance, a plain function, or as a MeshFunction instance. In the latter case, a 4th argument is provided to describe which subdomain number that describes the relevant boundary.
TestFunction(V): define a test function on a space V to be used in a variational form.
TrialFunction(V): define a trial function on a space V to be used in a variational form to represent the unknown in a finite element problem.
assemble(X): assemble a matrix, a right-hand side, or a functional, given a from X written with UFL syntax.
assemble_system(a, L, bcs): assemble the matrix and the right-hand side from a bilinear (a) and linear (L) form written with UFL syntax. The bcs parameter holds one or more DirichletBC objects.
LinearVariationalProblem(a, L, u, bcs): define a variational problem, given a bilinear (a) and linear (L) form, written with UFL syntax, and one or more DirichletBC objects stored in bcs.
LinearVariationalSolver(problem): create solver object for a linear variational problem object (problem).
solve(A, U, b): solve a linear system with A as coefficient matrix (Matrix object), U as unknown (Vector object), and b as right-hand side (Vector object). Usually, U = u.vector(), where u is a Function object representing the unknown finite element function of the problem, while A and b are computed by calls to assemble or assemble_system.
plot(q): quick visualization of a mesh, function, or mesh function q, using the Viper component in FEniCS.
interpolate(func, V): interpolate a formula or finite element function func onto the function space V.
project(func, V): project a formula or finite element function func onto the function space V.
When defining a function in terms of a mathematical expression inside a string formula, e.g.,
myfunc = Expression('sin(x[0])*cos(x[1])')
the expression contained in the first argument
will be turned into a C++ function
and compiled to gain efficiency. Therefore,
the syntax used in the expression must be valid C++ syntax.
Most Python syntax for mathematical expressions are also valid C++ syntax,
but power expressions make an exception: p**a must be written as
pow(p,a) in C++ (this is also an alternative Python syntax).
The following mathematical functions can be used directly
in C++
expressions when defining Expression objects:
cos, sin, tan, acos, asin,
atan, atan2, cosh, sinh, tanh, exp,
frexp, ldexp, log, log10, modf,
pow, sqrt, ceil, fabs, floor, and fmod.
Moreover, the number 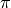 is available as the symbol pi.
All the listed functions are taken from the cmath C++ header file, and
one may hence
consult documentation of cmath for more information on the
various functions.
is available as the symbol pi.
All the listed functions are taken from the cmath C++ header file, and
one may hence
consult documentation of cmath for more information on the
various functions.
Parameters in expression strings must be initialized via keyword arguments when creating the Expression object:
myfunc = Expression('sin(w_x*x[0])*cos(w_y*x[1])',
w_x=pi, w_y=2*pi)
The following solution methods for linear systems can be accessed in FEniCS programs:
| Name | Method |
|---|---|
| 'lu' | sparse LU factorization (Gaussian elim.) |
| 'cholesky' | sparse Cholesky factorization |
| 'cg' | Conjugate gradient method |
| 'gmres' | Generalized minimal residual method |
| 'bicgstab' | Biconjugate gradient stabilized method |
| 'minres' | Minimal residual method |
| 'tfqmr' | Transpose-free quasi-minimal residual method |
| 'richardson' | Richardson method |
Possible choices of preconditioners include
| Name | Method |
|---|---|
| 'none' | No preconditioner |
| 'ilu' | Incomplete LU factorization |
| 'icc' | Incomplete Cholesky factorization |
| 'jacobi' | Jacobi iteration |
| 'bjacobi' | Block Jacobi iteration |
| 'sor' | Successive over-relaxation |
| 'amg' | Algebraic multigrid (BoomerAMG or ML) |
| 'additive_schwarz' | Additive Schwarz |
| 'hypre_amg' | Hypre algebraic multigrid (BoomerAMG) |
| 'hypre_euclid' | Hypre parallel incomplete LU factorization |
| 'hypre_parasails' | Hypre parallel sparse approximate inverse |
| 'ml_amg' | ML algebraic multigrid |
Many of the choices listed above are only offered by a specific backend, so setting the backend appropriately is necessary for being able to choose a desired linear solver or preconditioner.
An up-to-date list of the available solvers and preconditioners in FEniCS can be produced by
list_linear_solver_methods()
list_krylov_solver_preconditioners()
The linear algebra backend determines the specific data structures that are used in the Matrix and Vector classes. For example, with the PETSc backend, Matrix encapsulates a PETSc matrix storage structure, and Vector encapsulates a PETSc vector storage structure. Sometimes one wants to perform operations directly on (say) the underlying PETSc objects. These can be fetched by
A_PETSc =
down_cast(A).mat() b_PETSc = down_cast(b).vec() U_PETSc =
down_cast(u.vector()).vec()
Here, u is a Function, A is a Matrix, and b is a Vector. The same syntax applies if we want to fetch the underlying Epetra, uBLAS, or MTL4 matrices and vectors.
Sometimes one wants to implement tailored solution algorithms, using
special features of the underlying numerical packages.
Here is an example where we create an ML preconditioned Conjugate
Gradient solver by programming with Trilinos-specific objects directly.
Given a linear system
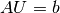 , represented by a Matrix object A,
and two Vector objects U and b in a
Python program, the purpose is to
set up a solver using the Aztec Conjugate Gradient method from
Trilinos’ Aztec library and combine that solver with the
algebraic multigrid preconditioner ML
from the ML library in Trilinos. Since the various parts of
Trilinos are mirrored in Python through the PyTrilinos package,
we can operate directly
on Trilinos-specific objects.
, represented by a Matrix object A,
and two Vector objects U and b in a
Python program, the purpose is to
set up a solver using the Aztec Conjugate Gradient method from
Trilinos’ Aztec library and combine that solver with the
algebraic multigrid preconditioner ML
from the ML library in Trilinos. Since the various parts of
Trilinos are mirrored in Python through the PyTrilinos package,
we can operate directly
on Trilinos-specific objects.
try:
from PyTrilinos import Epetra, AztecOO, TriUtils, ML
except:
print '''You Need to have PyTrilinos with'
Epetra, AztecOO, TriUtils and ML installed
for this demo to run'''
exit()
from dolfin import *
if not has_la_backend('Epetra'):
print 'Warning: Dolfin is not compiled with Trilinos'
exit()
parameters['linear_algebra_backend'] = 'Epetra'
# create matrix A and vector b in the usual way
# u is a Function
# Fetch underlying Epetra objects
A_epetra = down_cast(A).mat()
b_epetra = down_cast(b).vec()
U_epetra = down_cast(u.vector()).vec()
# Sets up the parameters for ML using a python dictionary
ML_param = {"max levels" : 3,
"output" : 10,
"smoother: type" : "ML symmetric Gauss-Seidel",
"aggregation: type" : "Uncoupled",
"ML validate parameter list" : False
}
# Create the preconditioner
prec = ML.MultiLevelPreconditioner(A_epetra, False)
prec.SetParameterList(ML_param)
prec.ComputePreconditioner()
# Create solver and solve system
solver = AztecOO.AztecOO(A_epetra, U_epetra, b_epetra)
solver.SetPrecOperator(prec)
solver.SetAztecOption(AztecOO.AZ_solver, AztecOO.AZ_cg)
solver.SetAztecOption(AztecOO.AZ_output, 16)
solver.Iterate(MaxIters=1550, Tolerance=1e-5)
plot(u)
The FEniCS software components are available for Linux, Windows and Mac OS X platforms. Detailed information on how to get FEniCS running on such machines are available at the fenicsproject.org website. Here are just some quick descriptions and recommendations by the author.
To make the installation of FEniCS as painless and reliable as possible, the reader is strongly recommended to use Ubuntu Linux. (Even though Mac users now can get FEniCS by a one-click install, I recommend using Ubuntu on Mac, unless you have high Unix competence and much experience with compiling and linking C++ libraries on Mac OS X.) Any standard PC can easily be equipped with Ubuntu Linux, which may live side by side with either Windows or Mac OS X or another Linux installation. Basically, you download Ubuntu from www.ubuntu.com/getubuntu/download, burn the file on a CD or copy it to a memory stick, reboot the machine with the CD or memory stick, and answer some usually straightforward questions (if necessary). On Windows, Wubi is a tool that automatically installs Ubuntu on the machine. Just give a user~name and password for the Ubuntu installation, and Wubi performs the rest. The graphical user interface (GUI) of Ubuntu is quite similar to both Windows 7 and Mac OS X, but to be efficient when doing science with FEniCS this author recommends to run programs in a terminal window and write them in a text editor like Emacs or Vim. You can employ an integrated development environment such as Eclipse, but intensive FEniCS developers and users tend to find terminal windows and plain text editors more user friendly.
Instead of making it possible to boot your machine with the Linux Ubuntu operating system, you can run Ubuntu in a separate window in your existing operation system. There are several solutions to chose among: the free VirtualBox and VMWare Player, or the commercial tools VMWare Fusion and Parallels (just search for the names to download the programs).
Once the Ubuntu window is up and running, FEniCS is painlessly installed by
sudo apt-get install fenics
Sometimes the FEniCS software in a standard Ubuntu installation lacks some recent features and bug fixes. Visiting the detailed download page on fenicsproject.org and copying a few Unix commands is all you have to do to install a newer version of the software.
Expressions and variational forms in a FEniCS program need to be compiled to C++ and linked with libraries if the expressions or forms have been modified since last time they were compiled. The tool Instant, which is part of the FEniCS software suite, is used for compiling and linking C++ code so that it can be used with Python.
Sometimes the compilation fails. You can see from the series of error messages which statement in the Python program that led to a compilation problem. Make sure to scroll back and identify whether the problematic line is associated with an expression, variational form, or the solve step.
The final line in the output of error messages points to a log file from the compilation where one can examine the error messages from the compiler. It is usually the last lines of this log file that are of interest. Occasionally, the compiler’s message can quickly lead to an understanding of the problem. A more fruitful approach is normally to examine the below list of common compilation problems and their remedies.
Instant remembers information about previous compilations and versions of your program. Sometimes removal of this information can solve the problem. Just run
instant-clean
in a terminal window.
If the compilation problem arises from line with an Expression object, examine the syntax of the expression carefully. The section User-Defined Functions contains some information on valid syntax. You may also want to examine the log file, pointed to in the last line in the output of error messages. The compiler’s message about the syntax problem may lead you to a solution.
Some common problems are
- using a**b for exponentiation (illegal in C++) instead of pow(a, b),
- forgetting that the spatial coordinates are denoted by a vector x,
- forgetting that the
,
, and
coordinates in space correspond to x[0], x[1], and x[2], respectively.
Failure to initialize parameters in the expressions lead to a compilation error where this problem is explicitly pointed out.
Sometimes the problem lies in the solve step where a variational form is turned into a system of algebraic equations. The error message “Unable to extract all indicies” points to a problem with the variational form. Common errors include
- missing either the TrialFunction or the TestFunction object,
- no terms without TrialFunction objects.
- mathematically invalid operations in the variational form.
The first problem implies that one cannot make a matrix system or system of nonlinear algebraic equations out of the variational form. The second problem means that there is no “right-hand side” terms in the PDE with known quantities. Sometimes this is seemingly the case mathematically because the “right-hand side” is zero. Variational forms must represent this case as Constant(0)*v*dx where v is a TestFunction object. An example of the third problem is to take the inner product of a scalar and a vector (causing in this particular case the error message to be “Shape mismatch”).
On Ubuntu Linux unfinished updates of the system (run by Update Manager) may causes all compilations to fail. When previously working programs no longer can be compiled, reboot Ubuntu, run the Update Manager, and wait until it has finished. Try compiling a working program again.
There are a large number of books on the finite element method. The books typically fall in either of two categories: the abstract mathematical version of the method and the engineering “structural analysis” formulation. FEniCS builds heavily on concepts in the abstract mathematical exposition. An easy-to-read book, which provides a good general background for using FEniCS, is Gockenbach [Gockenbach2006]. The book by Donea and Huerta [DoneaHuerta2003] has a similar style, but aims at readers with interest in fluid flow problems. Hughes [Hughes1987] is also highly recommended, especially for those interested in solid mechanics and heat transfer applications.
Readers with background in the engineering “structural analysis” version of the finite element method may find Bickford [Bickford1994] as an attractive bridge over to the abstract mathematical formulation that FEniCS builds upon. Those who have a weak background in differential equations in general should consult a more fundamental book, and Eriksson {em et al}. [ErikssonEstepHansboEtAl1996] is a very good choice. On the other hand, FEniCS users with a strong background in mathematics and interest in the mathematical properties of the finite element method, will appreciate the texts by Brenner and Scott [BrennerScott2008], Braess [Braess2007], Ern and Guermond [ErnGuermond2004], Quarteroni and Valli [QuarteroniValli1994], or Ciarlet [Ciarlet2002].
Two very popular introductory books on Python are “Learning Python” by Lutz [Lutz2007] and “Practical Python” by Hetland [Hetland2002]. More advanced and comprehensive books include “Programming Python” by Lutz [Lutz2006], and “Python Cookbook” [MartelliAscher2005] and “Python in a Nutshell” [Martelli2006] by Martelli. The web page http://wiki.python.org/moin/PythonBooks lists numerous additional books. Very few texts teach Python in a mathematical and numerical context, but the references [Langtangen2008] [Langtangen2009a] [Kiusalaas2005] are exceptions.
The author is very thankful to Johan Hake, Anders Logg, Kent-Andre Mardal, and Kristian Valen-Sendstad for promptly answering all my questions about FEniCS functionality and for implementing all my requests. I will in particular thank Professor Douglas Arnold for very valuable feedback on the text. Øystein Sørensen pointed out a lot of typos and contributed with many helpful comments. Many errors and typos were also reported by Mauricio Angeles, Ida Drøsdal, Hans Ekkehard Plesser, and Marie Rognes. Ekkehard Ellmann as well as two anonymous reviewers provided a series of suggestions and improvements.
The author is very thankful to Johan Hake, Anders Logg, Kent-Andre Mardal, and Kristian Valen-Sendstad for promptly answering all my questions about FEniCS functionality and for implementing all my requests. I will in particular thank Professor Douglas Arnold for very valuable feedback on the text. Øystein Sørensen pointed out a lot of typos and contributed with many helpful comments. Many errors and typos were also reported by Mauricio Angeles, Ida Drøsdal, Hans Ekkehard Plesser, and Marie Rognes. Ekkehard Ellmann as well as two anonymous reviewers provided a series of suggestions and improvements.